并查集

总概

  1. 合并两个集合
  2. 查询某个节点的祖宗的节点
    • 记录每个集合的大小：（绑定到根节点）
    • 每个节点到根节点的距离：（绑定到每个节点上）

1250. 格子游戏

题目链接：

1250. 格子游戏

题解思路：

根据题目，将各个元素映射到一维数组中，连接起来，检查连接的过程中是否出现环（若出现环状-》出现连接的时候两个节点在同一个连通块中）就说明有圈了

题目代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include <bits/stdc++.h>

using namespace std;

const int N = 41000;
int p[N];
int n, m;
int get(int x, int y){
    return x * n + y;
    //如果是第二种初始化的话可以按照数据来乘倍率
    /*
    return x * 200 + y;
    */
}

int find(int x){
    if(p[x] != x) p[x] = find(p[x]); //只有根节点的p[x] == x，所以继续找
    return p[x];
}

int main ()
{
    
    cin >> n >> m;
    int res = 0;
    for(int i = 0; i < n * n; i++) p[i] = i; //初始化
    /*
    从头初始化到结尾,第二种初始化
    for(int i = 1; i < N; i++)p[i] = i;
    */
    for(int i = 1; i <= m; i++){
        int x, y;
        char d;
        cin >> x >> y >> d;
        int a, b;
        //因为输入原因(初始化原因)以及get函数x,y需要从0开始，如果按第二种初始化就不用，也可以不用从0开始
        x--, y--;   
        a = get(x, y);
        if(d == 'D') b = get(x + 1, y);
        else b = get(x, y + 1);
        int pa = find(a), pb = find(b); 
        if(pa == pb){       //父亲节点相等就说明在同一个连通块中，连线必定有环
            res = i; break;
        }
        p[pa] = pb;
    }
    if(!res)cout << "draw" << endl;
    else cout << res << endl;
    return 0;
}

1252. 搭配购买

题目链接：

1252. 搭配购买 - AcWing题库

题解思路：

思路：根据题目，将各个搭配连接起来，就相当于各个连通块选择，使得总价为vol，价值最大的01背包问题

题目代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
/*
思路：根据题目，将各个搭配连接起来，就相当于各个连通块选择，使得总价为vol，价值最大的01背包问题
*/


#include <bits/stdc++.h>

using namespace std;
const int N = 10010;
int v[N], w[N], p[N], f[N];         // v[N] —— 价格、w[N] —— 价值、f[N] —— dp
int n, m, vol;

int find(int x){
    if(p[x] != x) p[x] = find(p[x]); // 祖宗节点的p[x] == x,持续向上查找到祖宗节点
    return p[x];
}

int main ()
{
    cin >> n >> m >> vol;
    for(int i = 1; i <= n; i++) cin >> v[i] >> w[i];
    for(int i = 1; i <= n; i++) p[i] = i;
    while(m --){
        int a, b;
        cin >> a >> b;
        int pa = find(a), pb = find(b);
        if(pa != pb){
            v[pb] += v[pa]; //总价格全部绑定到祖宗节点上去
            w[pb] += w[pa]; //总价值全部绑定到祖宗节点上去
            p[pa] = p[pb];  //pa的祖宗是pb
        }
    }
    
    // 01背包问题
    for(int i = 1; i <= n; i++){
        if(p[i] == i) //如果是祖宗节点，才进行状态转移（只有祖宗节点是这个连通块的总量）
            for(int j = vol; j >= v[i]; j--){
                f[j] = max(f[j], f[j - v[i]] + w[i]);  //状态转移
            }
    }
    cout << f[vol] << endl;
    return 0;
}

237. 程序自动分析

题目链接：

237. 程序自动分析

题解思路：

离散化+并查集

因为i,j的范围是1~1e9,所以需要离散化，然后就是基本的，相等的点连接到一个连通图里面，不相等的点进行判断。

离散化：

  1. 保序：排序+判重+二分
  2. 不保序： map、hash表

此题不保序

题目代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
/*
因为i,j的范围是1~1e9,所以需要离散化，然后就是基本的，相等的点连接到一个连通图里面，不相等的点进行判断。
*/


#include <bits/stdc++.h>

using namespace std;
const int N = 200010;
int n, m, p[N];
unordered_map<int, int> mp; //散列表
struct Q{
    int x, y, e;
}q[N];

int find(int x){
    if(p[x] != x)p[x] = find(p[x]);
    return p[x];
}

//离散化
int get(int x){
    if(mp.count(x) == 0) mp[x] = ++n; 
    return mp[x]; //返回离散化后对应的值
}

int main ()
{
    int T;
    cin >> T;
    while(T--){
        cin >> m;
        n = 0;
        mp.clear();
        
        //离散化各个点
        for(int i = 1; i <= m; i++ ){
            int x, y, e;
            cin >> x >> y >> e;
            q[i] = {get(x), get(y), e};
        }
        
        //初始化
        for(int i = 1; i <= n; i++) p[i] = i;
        
        //处理相等的值，将相等的值连接到一个连通块
        for(int i = 1; i <= m; i++){
            if(q[i].e == 1){
                //cout << q[i].x << " " << q[i].y << endl;
                int pa = find(q[i].x), pb = find(q[i].y);
                p[pa] = pb;
            }
        }
        int flag = 0;
        
        //非相等的值判断是否在同一个连通块中
        for(int i = 1; i <= m; i++){
            if(q[i].e == 0){
                int pa = find(q[i].x), pb = find(q[i].y);
                if(pa == pb) {
                    flag = 1;
                    break;
                }
            }
        }
        if(flag)cout << "NO" << endl;
        else cout << "YES" << endl;
    }
    return 0;
}

238. 银河英雄传说

题目链接：

238. 银河英雄传说

题解思路：

并查集：统一维护每个战舰到排头战舰的距离

当我们询问两个战舰间隔的时候是，|dx - dy| - 1 or 0(特判)

  1. 让排头当根节点->同时维护一个size表示当前队列的长度
  2. 假设有一个初始的队列a,新加一个队列b，就把队列b的排头d[b]+size[a]，并且在find函数里面刷新后面所有d[x];
  3. d[x]表示的是x到p[x]的距离，这样就可以很方便的算出每个节点到最排头的距离

题目代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

#include <bits/stdc++.h>

using namespace std;
const int N = 30010;
int p[N], d[N], Size[N], T;

int find(int x){
    if(p[x] != x){
        int root = find(p[x]);  //持续向上找到根节点
        d[x] += d[p[x]];        //会更新当前节点到根节点的距离
        p[x] = root;            //向上找到根节点
    }
    return p[x];
}

int main ()
{
    cin >> T;
    //初始化
    for(int i = 1; i < N; i++) p[i] = i, Size[i] = 1;
    while(T--){
        char op;
        int a, b;
        cin >> op >> a >> b;
        if(op == 'M'){
            int pa = find(a), pb = find(b);
            d[pa] = Size[pb];       //距离pb的距离
            Size[pb] += Size[pa];   //将a这一列的大小加到b这一列
            p[pa] = pb;             //pa的父节点是pb
        }else{
            int pa = find(a), pb = find(b);
            if(pa != pb){           //不在同一列
                cout << "-1" << endl;
            }else{                  //在同一列
                if(a != b)          //不是同一个节点
                    cout << abs(d[a] - d[b]) - 1 << endl;
                else cout << 0 << endl;
            }
            
        }
    }
}

239. 奇偶游戏

题目链接：

239. 奇偶游戏

题解思路：

总思想：前缀和

前缀和思想，如果是[l, r]内有奇数个1的话那么必有S[r] - S[l-1]为奇数，也即是S[r]、S[l - 1]奇偶性不同

同理如果是[l, r]内有偶数个1的话那么必有S[r] - S[l-1]为偶数，也即是S[r]、S[l - 1]奇偶性相同

方法一（扩展域）

枚举思想：

  1. 假设这个节点a是偶，并添加一个节点是a+M是奇
  2. 奇偶性相同的放在同一个集合中去
  3. 如果一组数据中，类型是偶数，就判断 a与b+M在不在同一个集合中
    • 在同一个集合中说明矛盾
    • 不在同一个集合中说明不矛盾
  4. 如果一组数据中，类型是奇数，就判断a与b是否在同一个集合中
    • 在同一个集合中说明，矛盾
    • 不在同一个集合中说明不矛盾

方法二（带边权）

维护一个带边权的并查集

  1. d[x]表示x与p[x]的关系
    • 0表示同类
    • 1表示不同类
  2. x与y是同类
    • p[x] = p[y]
      • d[x] ^ d[y]是0无矛盾，d[x]^d[y]是1有矛盾
    • p[x] != p[y]
      • d[p[x]] = d[x] ^ d[y]
  3. xy异类
    • p[x] = p[y]
      • d[x] ^ d[y]是0有矛盾，d[x]^d[y]是1无矛盾
    • p[x] != p[y]
      • d[p[x]] = d[x] ^ d[y] ^ 1
  4. 综上所述，就相当于代边权一个路径d表示x与根节点的关系，在find函数中需要对d进行更新类似于238题

题目代码：

方法一 （扩展域）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include <bits/stdc++.h>

using namespace std;
const int N = 41000, M = N / 2;
int p[N], n, m;
unordered_map<int, int> mp;

int find(int x){
    if(p[x] != x)p[x] = find(p[x]);
    return p[x];
}

//离散化
int get(int x){
    if(mp.count(x) == 0) mp[x] = ++n;
    return mp[x];
}

int main ()
{
    cin >> n >> m;
    n = 0;
    
    //初始化
    for(int i = 0; i < N; i++) p[i] = i;
    
    int res = m;
    for(int i = 1; i <= m; i++){
        string t;   //类型（奇偶）
        int a, b;
        cin >> a >> b >> t; 
        a = get(a - 1), b = get(b);     //相当于奇偶性~（Sl-1, Sr）
        if(t == "even"){                //奇偶性相同
            if(find(a) == find(b + M)){ //必然b+M与a的奇偶性就不能相同
                res = i - 1;            
                break;
            } 
            p[find(a)] = find(b);
            p[find(a + M)] = find(b + M);
        }else{                          //奇偶性不同
            if(find(a) == find(b)){     //那么奇偶性必然不能相同
                res = i - 1;
                break;
            }
            p[find(a)] = find(b + M);   //奇偶性相同的点加入到同一个集合中
            p[find(a + M)] = find(b);
        }
    }
    cout << res << endl;
    return 0;
}

方法二（带边权）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include <bits/stdc++.h>

using namespace std;
const int N = 41000, M = N / 2;
int p[N], d[N], n, m;
unordered_map<int, int> mp;

int find(int x){
    if(p[x] != x){
        int root = find(p[x]);
        d[x] += d[p[x]] % 2; //奇偶性原因，不影像最后结果，同时也防止爆int
        p[x] = root;
    }
    return p[x];
}

//离散化
int get(int x){
    if(mp.count(x) == 0) mp[x] = ++n;
    return mp[x];
}

int main ()
{
    cin >> n >> m;
    n = 0;
    
    //初始化
    for(int i = 0; i < N; i++) p[i] = i;
    
    int res = m;
    for(int i = 1; i <= m; i++){
        string t;   //类型（奇偶）
        int a, b;
        cin >> a >> b >> t; 
        a = get(a - 1), b = get(b);     //相当于奇偶性~（Sl-1, Sr）
        if(t == "even"){                //奇偶性相同
            int pa = find(a), pb = find(b);
            if(pa == pb){               //在同一集合中
                if((d[a] ^ d[b]) % 2){  //防止爆int
                    res = i - 1;
                    break;
                }
            }
            else{
                p[pa] = pb;
                d[pa] = d[a] ^ d[b];
            }
        }else{                              //奇偶性不同
            int pa = find(a), pb = find(b);
            if(pa == pb){                   //在同一集合中
                if((d[a] ^ d[b]) % 2 == 0){ //防止爆int
                    res = i - 1;
                    break;
                }
            }
            else{
                p[pa] = pb;
                d[pa] = d[a] ^ d[b] ^ 1;
            }
        }
    }
    cout << res << endl;
    return 0;
}

树状数组

原理

引入问题
给出一个长度为n的数组，完成以下两种操作：

  1. 将第i个数加上k
  2. 输出区间[i,j]内每个数的和

朴素算法

单点修改：O(1)
区间查询：O(n)

树状数组

快速求前缀和

单点修改：O(logn)
区间查询：O(logn)

lowbit()

lowbit()运算：x & (-x) 的用途一般是用来获取某个二进制数的 LowBit ，在树状数组中会用到
lowbit(x)是x的二进制表达式中最低位的1所对应的值.

1
2
3
4
int lowbit(int x)
{
    return x & -x;
}

树状数组思想

树状数组的本质思想是使用树结构维护”前缀和”，从而把时间复杂度降为O(logn)。

对于一个序列，对其建立如下树形结构：

  • 每个结点t[x]保存以x为根的子树中叶结点值的和
  • 每个结点覆盖的长度为lowbit(x)
  • t[x]结点的父结点为t[x + lowbit(x)]
  • 树的深度为log2n+1log2n+1

树状数组操作

add(x, k)表示将序列中第x个数加上k。

以add(3, 5)为例：
在整棵树上维护这个值，需要一层一层向上找到父结点，并将这些结点上的t[x]值都加上k，这样保证计算区间和时的结果正确。时间复杂度为O(logn)。

1
2
3
4
5
void add(int x, int k)
{
    for(int i = x; i <= n; i += lowbit(i))
        t[i] += k;
}

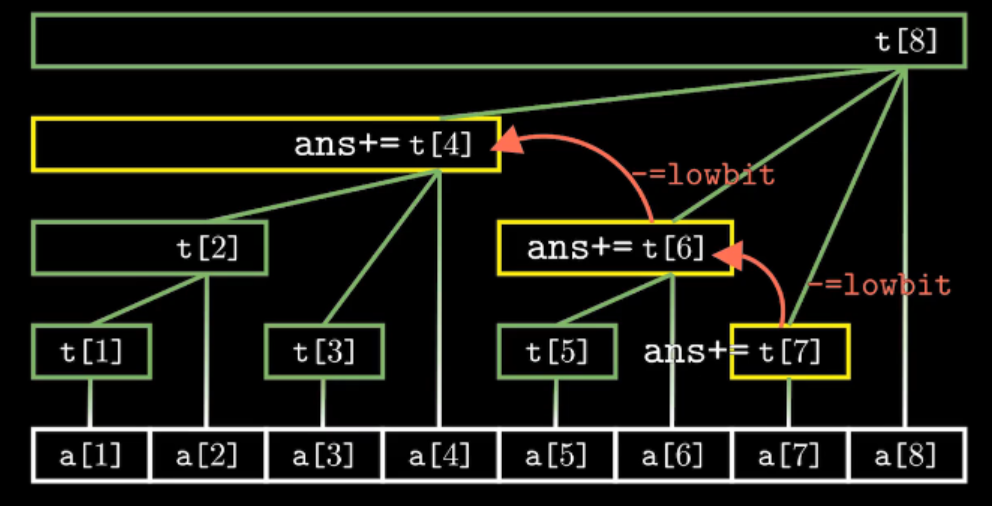
ask(x)表示将查询序列前x个数的和

以ask(7)为例：
查询这个点的前缀和，需要从这个点向左上找到上一个结点，将加上其结点的值。向左上找到上一个结点，只需要将下标 x -= lowbit(x)，

例如 7 - lowbit(7) = 6。

1
2
3
4
5
6
7
int ask(int x)
{
    int sum = 0;
    for(int i = x; i; i -= lowbit(i))
        sum += t[i];
    return sum;
}

树状数组初始化

若给你一个数组，时间卡的特别紧的话，需要O(n)的时间复杂度去初始化树状数组，那么可以On求出前缀和数组S

tr[x] = S[x] - S[x - lowbit(x)]

上述介绍引用：qiaoxinwei

241. 楼兰图腾

题目链接：

241. 楼兰图腾

题解思路：

树状数组

  1. tr[x]保存数据在[1, x]的个数，t[r] - t[l-1]代表在[l, r]之间数据的个数
  2. Greater[i]表示前i个数里面有多少个比a[i]大的数、Lower[i]表示前i个数里面有多少个比a[i]小的数
  3. 以i为中心，左边大于i的*右边大于i的就是以当前i为中心的所有V个数

题目代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
const int N = 210000;
int a[N], tr[N], Greater[N], Lower[N], n;

int lowbit(int x){
    return x & -x;
}

void add(int x, int c){
    for(int i = x; i <= n; i += lowbit(i)) tr[i] += c;  //从前往后遍历更新将会影响到后面所有的tr
}

int sum(int x){
    int res = 0;
    for(int i = x; i; i -= lowbit(i)) res += tr[i]; //从后往前遍历减去末位1所对应的值
    return res;
}

int main ()
{
    scanf("%d", &n);
    for(int i = 1; i <= n; i++){
        scanf("%d", &a[i]);
    }
    
    for(int i = 1; i <= n; i++){
        int y = a[i];
        Greater[i] = sum(n) - sum(y);   //前i个元素中，在[y + 1, n]范围的个数
        Lower[i] = sum(y - 1);          //前i个元素中， 在[1, y - 1]范围的个数
        add(y, 1);      //添加y,个数为1
    }
    
    memset(tr, 0, sizeof tr);       //初始化一下变成0,因为后续操作需要从右边往左遍历
    ll res1 = 0, res2 = 0;
    for (int i = n; i; i -- )
    {
        int y = a[i];
        res1 += Greater[i] * (ll)(sum(n) - sum(y)); //[i + 1, n]元素中，在[y + 1, n]范围的个数
        res2 += Lower[i] * (ll)(sum(y - 1));        //[i + 1, n]元素中， 在[1, y - 1]范围的个数
        add(y, 1);
    }

    printf("%lld %lld\n", res1, res2);
    return 0;
    
}

242. 一个简单的整数问题

题目链接：

242. 一个简单的整数问题

题解思路：

树状数组+差分

  1. 根据题目意思在a数组的[l, r]区间每个元素加d，可以求a数组的差分，然后对a数组的差分来求树状数组
  2. 可以根据a数组的差分来求的树状数组，来还原a数组

题目代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include <bits/stdc++.h>

typedef long long ll;

using namespace std;

const int N = 100010;
int a[N], n, m;
ll  tr[N];
int lowbit(int x){
    return x & -x;
}

void add(int x, int c){
    for(int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}

ll sum(int x){
    ll s = 0;
    for(int i = x; i; i -= lowbit(i)) s += tr[i];
    return s;
}

int main ()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
    for(int i = 1; i <= n; i++) add(i, a[i] - a[i - 1]);    //求a数组差分的树状数组
    
    for(int i = 0; i < m; i++){
        char op[2];
        int l, r, d;
        scanf("%s", op);
        if(op[0] == 'Q'){
            scanf("%d", &l);
            printf("%lld\n", sum(l));   
        }else{
            scanf("%d%d%d", &l, &r, &d);
            add(l, d), add(r + 1, -d);
        }
    }
    return 0;
}

243. 一个简单的整数问题2

题目链接：

243. 一个简单的整数问题2

题解思路：

树状数组+差分

  1. 根据差分的思想，求出a的差分数组b

题目代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include <bits/stdc++.h>
typedef long long ll;
using namespace std;
const int N = 100010;
ll tr1[N], tr2[N];  // b的前缀和， b * i 的前缀和
int n, m, a[N];     //b是a的差分

int lowbit(int x){
    return x & -x;
}

void add(ll tr[], int x, ll c){
    for(int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}

ll sum(ll tr[], int x){
    ll s = 0;
    for(int i = x; i; i -= lowbit(i)) s += tr[i];
    return s;
}

ll pre_sum(int x){
    return sum(tr1, x) * (x + 1) - sum(tr2, x);
}

int main ()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
    for(int i = 1; i <= n; i++) {
        int b = a[i] - a[i - 1];    //a数组的差分
        add(tr1, i, b);             //维护差分数组b
        add(tr2, i, (ll)b * i);     //维护b * i的树状数组
    }
    
    while(m --){
        char op[2];
        int l, r, d;
        scanf("%s%d%d", op, &l, &r);
        if(op[0] == 'Q'){
            printf("%lld\n", pre_sum(r) - pre_sum(l - 1));  //更具推出来的公式
        }else{
            scanf("%d", &d);
            add(tr1, l, d), add(tr1, r + 1, -d);            
            add(tr2, l, d * l), add(tr2, r + 1, -d * (r + 1));
        }
    }
    return 0;
}

244. 谜一样的牛

题目链接：

244. 谜一样的牛

题解思路：

树状数组+二分查找

  1. 根据观察发现最后一头牛可以确定：最后一头牛前面有k个比它矮的牛，那么它必定是第k+1矮的牛
  2. 所以从后往前遍历，每次确定最后一头牛，他当前高度必定是剩下的牛种第k+1矮的（可以通过二分查找来确定每头牛的高度）
  3. 每确定一头牛，就删除这头牛的高度

题目代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <bits/stdc++.h>

using namespace std;
const int N = 100010;
int h[N], res[N], tr[N], n;

int lowbit(int x){
    return x & -x;
}

//加元素
void add(int x, int c){
    for (int i = x; i <= n; i += lowbit(i)) tr[i] += c;
}

//查询
int sum(int x){
    int s = 0;
    for (int i = x; i; i -= lowbit(i)) s += tr[i];
    return s;
}

int main()
{
    cin >> n;
    for (int i = 2; i <= n; i ++ ) scanf("%d", &h[i]);
    for (int i = 1; i <= n; i ++ ) tr[i] = lowbit(i);   //初始化tr，（每种高度的个数都是1）

    for (int i = n; i; i -- ) { //从后往前遍历,确定每一头牛的身高
        int k = h[i] + 1;		//这头牛的高度必定是剩下牛当中第k+1矮的
        int l = 1, r = n;
        while (l < r) {         //二分查找剩下的数中第一个等于k的，就是当前牛的高度
            int mid = (l + r) >> 1;
            if (sum(mid) >= k) r = mid;
            else l = mid + 1;
        }
        res[i] = r;             //当前牛的高度
        add(r, -1);             //删除此高度
    }
    for (int i = 1; i <= n; i ++ ) printf("%d\n", res[i]);
    return 0;
}

线段树

操作原理

操作

  1. pushup(u)：子节点的信息更新父节点的信息。

  2. build()：将一段区间初始化成线段树。

  3. modify()：修改。

    • 单点：easy。

    • 区间：pushdown（懒标记）hard。

      • 类似于查询的时候，找到一个完整区间的时候直接标记一下（需要维护一个add）。

      • 维护一个add(懒标记)，以当前节点为根的子树中的每一个节点加上一个add（不包含根节点）。

      • 在pushdown的时候被标记的节点如果继续往下递归的话，就将当前节点的标记取消并且递归到子节点上，这样所有叶子节点的祖宗节点的标记已经取消掉，并且累加到此叶子节点上了。

        left.add += root.add, left.sum += (left.r - left.l + 1) * root.add

        right.add += root.add, right += (right.r - right.l + 1) * root.add

        root.add = 0

  4. query()：查询

    查询某一个子区间的时候一定要pushdown一下

基本知识

满二叉树

线段树一般开空间：4n

1. 最大数

题目链接：

最大数

题解思路：

线段树

  1. 用线段树维护区间最大值
  2. 查询时
    • [tr.l , tr.r] 属于 [l, r]直接返回[tr.l, tr.r]区间内维护的最大值即可
    • l <= mid说明有左边部分，递归往左边查询即可
    • r>mid说明有右边部分，递归往右边查询即可
  3. 修改时
    • 递归调用，直至叶节点，修改叶节点的值
    • pushup一下，将子节点的信息更新到父节点上

题目代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#include <bits/stdc++.h>

using namespace std;
typedef long long LL;
const int N = 200010;
int m, p;

// 一般开的空间大小为4*N
struct Node{
    int l, r;
    int v; //维护区间最大值
}tr[4*N];

void pushup(int u)  // 由子节点的信息，来计算父节点的信息
{
    tr[u].v = max(tr[u << 1].v, tr[u << 1 | 1].v);
}

//初始化线段树，u为当前线段树的节点编号
void build(int u, int l, int r){
    tr[u] = {l, r};
    if(l == r) return; //l == r说明是叶子节点直接退出
    int mid = l + r >> 1;
    build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
}

//查询以u为根节点，[l,r]中的最大值
int query(int u, int l, int r){
    //区间[tr[u].l, tr[u].r] 属于区间[l, r],直接返回就得到当前区间最大值
    if(tr[u].l >= l && tr[u].r <= r) return tr[u].v; 
    
    int mid = tr[u].l + tr[u].r >> 1;
    int v = 0;
    
    //左边
    if(l <= mid) v = query(u << 1, l , r); //往左边查询
    //右边
    if(r > mid) v = max(v, query(u << 1 | 1, l ,r)); //取右边与左边的最大值
    
    return v;
    
}


//u为节点为编号，更新该节点的最大值
void modify(int u, int x, int v) {
    if(tr[u].l == tr[u].r) tr[u].v = v;  //叶节点，递归出口
    else {
        int mid = tr[u].l + tr[u].r >> 1;
        //分治处理左右子树, 寻找x所在的子树
        if(x <= mid) modify(u << 1, x, v);
        else modify(u << 1 | 1, x, v);
        //pushup操作, 子结点的信息更新父节点
        pushup(u);
    }
}


int main ()
{
    int n = 0, last = 0; // n表示树中节点个数、last表示上一次操作
    cin >> m >> p;
    build(1, 1, m); //初始化线段树，节点的区间[1, m]
    
    while(m --){
        char op[2];
        cin >> op;
        if(op[0] == 'A'){       //添加结点
            int t;cin >> t;
            modify(1, n + 1, ((LL)t + last) % p); //在n + 1处插入   
            n++;    //结点个数+1
        }else{        //询问
            int L; cin >> L;
            last = query(1, n - L + 1, n); //查询[n - L + 1, n]内的最大值，u = 1，即从根节点开始查询
            cout << last << endl;
        }
    }
    return 0;
}

2. 你能回答这些问题吗

题目链接：

你能回答这些问题吗

题解思路：

思路：

  1. 维护四个数值：

    • tmax：最大连续子段和
    • lmax：最大前缀和
    • rmax：最大后缀和
    • sum：区间和

  2. 确定tmax:

    $tmax = max(left-son.tmax, right-son.tmax, left-son.rmax + right-son.lmax)$

  3. 确定lmax,rmax:

    以维护lmax为例：

    • 完全在左区间内：左边的lmax
    • 横跨两个区间：左边的sum+右边的lmax

    rmax同理

题目代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
#include <bits/stdc++.h>

using namespace std;
const int N = 500010;
int w[N], n, m;

struct Node{
    int l, r;
    int tmax, lmax, rmax, sum;  //维护最大连续子段和、最大前缀和、最大后缀和、区间和
}tr[4 * N];

void pushup(Node &u, Node &l, Node &r){
    u.sum = l.sum + r.sum;                              //区间和
    u.lmax = max(l.lmax, l.sum + r.lmax);               //前缀和等于两种请况取最大值（左区间的前缀和，左区间的sum + 右区间的前缀和）
    u.rmax = max(r.rmax, r.sum + l.rmax);               //后缀和同理
    u.tmax = max(max(l.tmax, r.tmax), l.rmax + r.lmax); //最大连续字段和取三种情况的最大和（左区间tmax,右区间tmax,在中间（左区间后缀+右区间前缀和））
}

void pushup(int u){
    pushup(tr[u], tr[u << 1], tr[u << 1 | 1]);
}

//初始化
void build(int u, int l, int r){
    //如果是叶节点,叶节点直接赋值
    if(l == r) tr[u] = {l, r, w[r], w[r], w[r], w[r]}; 
    else{
        tr[u] = {l , r};
        int mid = l + r >> 1;
        build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r); //递归建立左右子树
        pushup(u);  //子节点去更新父节点的信息
    }
}

//修改
void modify(int u, int x, int v){
    //如果到达叶节点
    if(tr[u].l == x && tr[u].r == x) tr[u] = {x, x, v, v, v, v};
    else{
        int mid = tr[u].l + tr[u].r >> 1;
        if(mid >= x)modify(u << 1, x, v);   //往左边递归
        else modify(u << 1 | 1, x, v);      //往右边递归
        pushup(u);      //更新
    }
}

//查询
Node query(int u, int l, int r){
    //查询区间包含当前线段树区间
    if(tr[u].l >= l && tr[u].r <= r) return tr[u];
    else{
        int mid = tr[u].l + tr[u].r >> 1;
        if(mid >= r) return query(u << 1, l, r);            //在左
        else if(l > mid) return query(u << 1 | 1, l, r);    //在右边
        else{                                               //横跨两个区间
            Node left = query(u << 1, l, r);            
            Node right = query(u << 1 | 1, l, r);
            Node res;
            pushup(res, left, right);
            return res;
        }
    }
}

int main ()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++)scanf("%d", &w[i]);
    build(1, 1, n);
    while(m--){
        int k, x, y;
        scanf("%d%d%d", &k, &x, &y);
        if(k == 1){
            if(x > y) swap(x, y);
            printf("%d\n", query(1, x, y).tmax);
        }else{
            modify(1, x, y);
        }
    }
}

3. 区间最大公约数

题目链接：

区间最大公约数

题解思路：

操作1：区间[l,r]增加一个数

操作2：区间[l,r]最大公约数

思路：

  1. 将区间增加一个数，转换为单点增加一个数，可以推出用差分。

  2. 证明差分数组和原数组某个区间内有共同的最大公因数。

    • ($a1,a_2,···，a_n$）= （$a_1,a_2-a_1,···，a_n-a{n-1} $）
    • gcd(a, b) = gcd(a, b - a)
    • gcd(a, b) = gcd(a, -b)

  3. 查询某个区间[l, r]的最大公约数

    $gcd(a[l], gcd(b[l + 1], b[r]))$

题目代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
#include <bits/stdc++.h>
typedef long long LL;

using namespace std;

const int N = 500100;

int n, m;        
LL w[N];
struct Node{
    int l, r;
    LL sum, d;
}tr[4 * N];

LL gcd(LL a, LL b)  //求最大公约数
{
    return b ? gcd(b, a % b) : a;
}

void pushup(Node &u, Node &l, Node &r)  //由子区间信息更新父区间信息
{
    u.sum = l.sum + r.sum;  // 区间和
    u.d = gcd(l.d, r.d);    //左右区间最大公约数
}

void pushup(int u)
{
    pushup(tr[u], tr[u << 1], tr[u << 1 | 1]);
}

//初始化
void build(int u, int l, int r)         
{
    tr[u].l = l, tr[u].r = r;
    if ( l == r ) 
        tr[u].d = w[l] - w[l - 1], tr[u].sum = w[l] - w[l - 1]; //将差分数组维护到线段树中去
    else
    {
        int mid = l + r >> 1;
        build(u << 1, l, mid);
        build(u << 1 | 1, mid + 1, r);
        pushup(u);      //更新
    }
}

//修改
void modify(int u, int x, LL v)         
{
    //叶节点
    if ( tr[u]. r == x && tr[u].l == x ) 
        tr[u].d = tr[u].sum + v, tr[u].sum += v;        
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;       
        if ( mid >= x ) modify(u << 1, x, v);   //修改左区间
        else modify(u << 1 | 1, x, v);          //修改右区间
        pushup(u);
    }
}

Node query(int u, int l, int r)
{
    //查询区间包含当前线段树区间
    if ( tr[u].l >= l && tr[u].r <= r ) return tr[u];   
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;
        if ( mid >= r ) return query(u << 1, l, r);
        else if ( mid < l ) return query(u << 1 | 1, l, r);
        else
        {
            Node left = query(u << 1, l, r);        //如果当前访问区间的子区间横跨询问区间
            Node right = query(u << 1 | 1, l, r);   //则递归两个子区间
            Node res;                               
            pushup(res, left, right);               //更新，相当于求right和left区间合并后的结果
            return res;
        }
    }
}

int main ()
{
    cin  >> n >> m;
    for(int i = 1; i <= n; i++)scanf("%lld", &w[i]);
    build(1, 1, n); //初始化
    char op[2];
    int l, r;
    LL d;
    while(m--){
        scanf("%s%d%d", op, &l, &r);
        if(op[0] == 'Q'){
            auto left = query(1, 1, l);     //求前缀和得到a[l]
            Node right({0, 0, 0, 0});
            if (l + 1 <= r) right = query(1, l + 1, r);
            printf("%lld\n", abs(gcd(left.sum, right.d)));  //gcd(a[l], gcd(b[l + 1], b[r]))
        }else{
            scanf("%lld", &d);
            modify(1, l, d);
            if ( r + 1 <= n ) modify(1, r + 1, -d);
        }
    }
    return 0;
}

4. 一个简单的整数问题2

题目链接：

一个简单的整数问题2

题解思路：

最基本的线段树做法（添加懒标记）

  • 类似于查询的时候，找到一个完整区间的时候直接标记一下（需要维护一个add）。

  • 维护一个add(懒标记)，以当前节点为根的子树中的每一个节点加上一个add（不包含根节点）。

  • 在pushdown的时候被标记的节点如果继续往下递归的话，就将当前节点的标记取消并且递归到子节点上，这样所有叶子节点的祖宗节点的标记已经取消掉，并且累加到此叶子节点上了。

    left.add += root.add, left.sum += (left.r - left.l + 1) * root.add

    right.add += root.add, right += (right.r - right.l + 1) * root.add

    root.add = 0

题目代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
#include <bits/stdc++.h>
typedef long long ll;

using namespace std;
const int N = 100010;
int w[N], n, m;

struct Node{
    int l, r;
    ll sum, add;
}tr[N * 4];

void pushup(int u){
    tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum; //左右儿子之和
}

void build(int u, int l, int r){
    if(l == r) tr[u] = {l, r, w[r], 0};
    else{
        tr[u] = {l, r};
        int mid = l + r >> 1;
        build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
        pushup(u); //更新
    }
}


void pushdown(int u){
    auto &root = tr[u], &left = tr[u << 1], &right = tr[u << 1 | 1];
    if(root.add){
        left.add += root.add, left.sum += (ll)(left.r - left.l + 1) * root.add;
        right.add += root.add, right.sum += (ll)(right.r - right.l + 1) * root.add;
        root.add = 0;
    }
}



//修改之前也需要pushdown()一下
void modify(int u, int l, int r, int d){
    if(tr[u].l >= l && tr[u].r <= r){
        tr[u].sum += (ll)(tr[u].r - tr[u].l + 1) * d;
        tr[u].add += d;
    }else{ //分裂的情况
        pushdown(u);
        int mid = tr[u].l + tr[u].r >> 1;
        if(l <= mid) modify(u << 1, l, r, d);
        if(r > mid) modify(u << 1 | 1, l, r, d);
        pushup(u);
    }
}



//查询之前一定要pushdown()一下
ll query(int u, int l, int r)
{
    if (tr[u].l >= l && tr[u].r <= r) return tr[u].sum;

    pushdown(u);
    int mid = tr[u].l + tr[u].r >> 1;
    ll sum = 0;
    if (l <= mid) sum = query(u << 1, l, r);
    if (r > mid) sum += query(u << 1 | 1, l, r);
    return sum;
}

int main ()
{
    cin >> n >> m;
    for(int i = 1; i <= n; i++) scanf("%d", &w[i]);
    
    build(1, 1, n);
    char op[2];
    int l, r, d;
    while(m --){
        scanf("%s%d%d", op, &l, &r);
        if(op[0] == 'C'){
            scanf("%d", &d);
            modify(1, l, r, d);
        }
        else printf("%lld\n", query(1, l, r));
    }
   
    return 0;
}

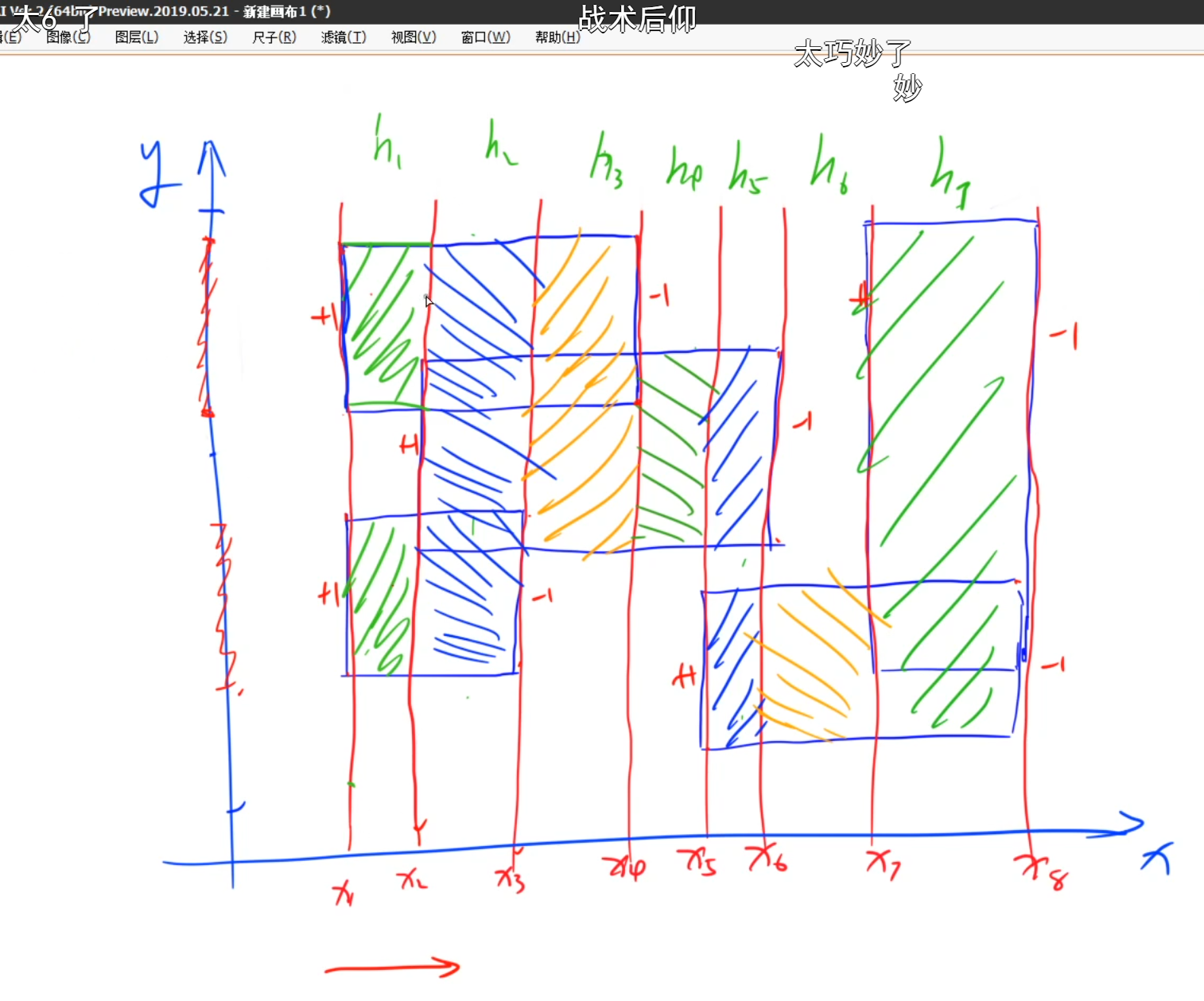
5. 亚特兰蒂斯

题目链接：

亚特兰蒂斯

题解思路：

线段树+扫描线+离散化

操作一：将某一个区间[l, r] + k

操作二：整个区间中权值大于0的总长是多少

需要用离散化去处理y坐标，但是线段树维护的是y这个区间。

线段树中的节点信息：

  1. cnt 当前区间整个被覆盖的次数
  2. len 不考虑祖先节点cnt的前提下cnt>0的区间总长

扫描线：

  1. 永远只考虑根节点的信息（说明在query的时候不需要pushdown）
  2. 所有操作都是成对出现，且先加后减

题目代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
#include <bits/stdc++.h>

using namespace std;

const int N = 100010;

vector<double>ys;//用于离散化
int n;

// 用来存线段信息
struct segment {
    double x, y1, y2;
    int d; // 区分它是该矩阵前面的线段还是后面的线段
    bool operator < (const segment&t)const
    {
        return x < t.x;
     } 
}seg[N * 2];//每个矩阵需要存两个线段

// 线段树的每个节点 保存的为线段, 0号点为y[0]到y[1]，以此类推
struct node {
    int l,r;
    int cnt;    // 记录当前区间整个被覆盖的次数
    double len; // 记录这段区间的长度
}tr[N * 8];     //由于线段二倍，所以8倍空间

// 返回第一个 >= y 的数的下标
int find(double y) {
    return lower_bound(ys.begin(), ys.end(), y) - ys.begin();
}

void pushup(int u) {
    if(tr[u].cnt)tr[u].len = ys[tr[u].r + 1] - ys[tr[u].l];//表示整个区间都被覆盖，该段长度就为右端点 + 1后在ys中的值 - 左端点在ys中的值
    else if(tr[u].l != tr[u].r){
        tr[u].len = tr[u << 1].len + tr[u << 1 | 1].len;
    }
    else tr[u].len = 0;//表示为叶子节点且该线段没被覆盖，为无用线段，长度变为0
}

void modify(int u,int l,int r,int d) {
    if(tr[u].l >= l && tr[u].r <= r) {
        tr[u].cnt += d;     
        pushup(u);          //更新该节点的len
    }else{
        int mid = tr[u].r + tr[u].l >> 1;
        if (l <= mid)modify(u << 1, l, r, d);      //左边存在点
        if (r > mid)modify(u << 1 | 1, l, r, d);   //右边存在点
        pushup(u);      //更新
    }
}

void build(int u,int l,int r){
    tr[u] = {l, r, 0, 0};
    if (l != r){
        int mid = l + r >> 1;
        build(u << 1,l,mid),build(u << 1 | 1,mid + 1,r);
        //后面都为0，不需更新len
    }
}

int main()
{
    int T = 1;
    while (cin >> n && n)
    {
        ys.clear();
        int j = 0;              //线段个数
        for (int i = 0 ; i < n ; i ++) {
            double x1,y1,x2,y2;
            cin>>x1>>y1>>x2>>y2;
            seg[j ++] = {x1, y1, y2, 1};        //前面的线段
            seg[j ++] = {x2, y1, y2, -1};       //后面的线段
            ys.push_back(y1), ys.push_back(y2);  //y轴出现过那些点
        }
        sort(seg,seg + j);          //线段按x排序

        //去重
        sort(ys.begin(),ys.end());  
        ys.erase(unique(ys.begin(),ys.end()),ys.end());//离散化去重

        build(1, 0, ys.size() - 2);

        double res = 0;
        for (int i = 0 ; i < j ; i ++) {
            if (i)res += tr[1].len * (seg[i].x - seg[i - 1].x); //根节点的长度即为此时有效线段长度 ，再 * x轴长度即为面积
            modify(1, find(seg[i].y1), find(seg[i].y2) - 1, seg[i].d);
        }

        printf("Test case #%d\n", T ++ );
        printf("Total explored area: %.2lf\n\n", res);
    }
    return 0;
}

6. 维护序列

题目链接：

维护序列

题解思路：

线段树需要维护的信息：

sum、add、mul 需要有两个懒标记，先乘再加，方便更新mul和add

只是基础线段树的一个拓展

题目代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
#include <bits/stdc++.h>

using namespace std;
typedef long long LL;
const int N = 100010;

int n, p, m;
int w[N];
struct Node {
    int l, r;
    int sum, add, mul;  //维护一个乘一个加,先乘后加使得便于维护
}tr[N * 4];

void pushup(int u) {
    tr[u].sum = (tr[u << 1].sum + tr[u << 1 | 1].sum) % p; 
}

void eval(Node &t, int add, int mul) {
    t.sum = ((LL)t.sum * mul + (LL)(t.r - t.l + 1) * add) % p; //计算总和
    t.mul = (LL)t.mul * mul % p;            //先乘后加使得便于维护
    t.add = ((LL)t.add * mul + add) % p;
}

//消除祖宗节点的标记
void pushdown(int u) {
    eval(tr[u << 1], tr[u].add, tr[u].mul); 
    eval(tr[u << 1 | 1], tr[u].add, tr[u].mul);
    tr[u].add = 0, tr[u].mul = 1;
}

void build(int u, int l, int r) {
    if (l == r) tr[u] = {l, r, w[r], 0, 1};
    else{
        tr[u] = {l, r, 0, 0, 1};
        int mid = l + r >> 1;
        build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
        pushup(u);  //更新
    }
}

void modify(int u, int l, int r, int add, int mul){
    if (tr[u].l >= l && tr[u].r <= r) eval(tr[u], add, mul);    //计算一下当前节点的值
    else{
        pushdown(u);
        int mid = tr[u].l + tr[u].r >> 1;
        if (l <= mid) modify(u << 1, l, r, add, mul);   //修改左右孩子
        if (r > mid) modify(u << 1 | 1, l, r, add, mul);
        pushup(u);
    }
}

int query(int u, int l, int r){
    if (tr[u].l >= l && tr[u].r <= r) return tr[u].sum;

    pushdown(u);
    int mid = tr[u].l + tr[u].r >> 1;
    int sum = 0;
    if (l <= mid) sum = query(u << 1, l, r);
    if (r > mid) sum = (sum + query(u << 1 | 1, l, r)) % p;
    return sum;
}

int main()
{
    cin >> n >> p;
    for (int i = 1; i <= n; i ++ ) scanf("%d", &w[i]);
    
    build(1, 1, n);
    cin >> m;
    while (m --) {
        int t, l, r, d;
        scanf("%d%d%d", &t, &l, &r);
        if (t == 1) {
            scanf("%d", &d);
            modify(1, l, r, 0, d);
        } else if (t == 2) {
            scanf("%d", &d);
            modify(1, l, r, d, 1);
        }
        else printf("%d\n", query(1, l, r));
    }

    return 0;
}

可持久化数据结构

  1. trie的可持久化
  2. 线段树的可持久化——主席树

可持久化的前提：本身拓扑结构、不变

解决的问题：将所有数据结构的历史版本都保存下来（有点像git）

核心思想：只记录每一个版本与前一个版本不同的节点

1. 最大异或和

题目链接：

最大异或和

题解思路：

  1. 求出前缀异或和，每次所求就是：$S{p-1}\ xor\ S{N}\ xor \ x = c$使得在l,r内c最大。
  2. 但是会有A操作在数组尾添加元素，这样就会影响到查询的结果，所有用可持久化维护各个版本，求[1, R]可用root[R]以及上述公式来求最大c。
  3. 但是同时又得求[L ,R]之内得最大c,所有需要trie维护一个信息，max-id（当前子树下标的最大值），只要当前子树下标最大值符合[L , R]就可以继续往当前子树查询。

题目代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
#include <cstdio>
#include <cstring>
#include <algorithm>

using namespace std;
// 30w初始数据和30w新增,  而10的7次方小于2的24次方, 再加上根节点, 就是说每个数最多需要25位;
const int N = 600010, M = N * 25;

int n, m;
int s[N]; // 前缀和序列
int tr[M][2];
int max_id[M];  // 用于记录当前根节点版本的最大id范围
int root[N], idx;

// i是第i个插入的数的i, p是上一个插入的数的节点号, q是当前节点号, k是现在取到第k位
void insert(int i, int k, int p, int q)
{
    // 如果记录结束了
    if (k < 0)
    {
        max_id[q] = i;  // 记录当前节点(可能会被后面公用)所能到达的最大范围i
        return;
    }

    // 取出前缀和的二进制表示从右往左数第k位v
    // 需要注意的是, 这个s[i]就是我们要存的东西!!!!!
    int v = s[i] >> k & 1;

    // 如果前一个节点存在当前节点没有的分支, 那就把当前节点的这个空的路径指过去, 这就相当于复制!
    if (p) tr[q][v ^ 1] = tr[p][v ^ 1];

    tr[q][v] = ++idx; // 现在才是正常trie树插入

    // 递归插入下一位二进制, tr[q][v]就是我们本轮插入的新节点
    // 而前面我们只复制了前一轮的不同v方向的路径, v方向的还没动过, 于是放到p里面等下一轮
    // 至于为什么可以放到下一轮, 因为当前q新插入的数字(二进制当前位)是v, 而p的这条路径也是v
    // 所以暂时不需要复制
    insert(i, k - 1, tr[p][v], tr[q][v]);

    // 下面是递归到所有点都插入完成才开始进行的, 所以能把最大max_id递归传递回去
    // 每个点的最大范围用子节点最大的值, 然后还能递归传递回去, 因为当前递归层
    // 的q, 就是上一层的tr[q][v], 观察易知每个节点都会有对应max_id
    max_id[q] = max(max_id[tr[q][0]], max_id[tr[q][1]]);
}

int query(int r, int C, int l)
{
    // 选用合适的root, 就是第r-1个节点作为root(-1已在传参前完成)
    // 然后根据异或的前缀和性质才能保证在r左边
    int p = root[r];

    for (int i = 23; i >= 0; i--)
    {
        // C是s[n] ^ x, 从高位到低位逐位检索二进制每一位上能跟C异或结果最大的数
        int v = C >> i & 1; 
        // 自带判空功能如果没有点, max_id会为0, 那就肯定不能满足>=l
        // 而max_id又同时可以限制当前的点是在l r区间内
        // 另外, 如果tr[p][v^1]为空, 那么tr[p][v]就肯定不为空,并在l r区间, 因为根据
        // 插入的代码, 每个节点至少有一条当前s[i]的完整路径
        // 而如果tr[p][v^1]不为空但maxid小于l, 同理也能选取到tr[p][v]
        if (max_id[tr[p][v ^ 1]] >= l) p = tr[p][v ^ 1]; 
        else p = tr[p][v];
    }

    return C ^ s[max_id[p]];
}

int main()
{
    scanf("%d%d", &n, &m);
    // 前缀和, 初始化root[0]
    max_id[0] = -1;
    root[0] = ++idx;
    insert(0, 23, 0, root[0]);
    for (int i = 1; i <= n; i++)
    {
        int x;
        scanf("%d", &x);
        s[i] = s[i - 1] ^ x; // 前缀和序列
        root[i] = ++idx;
        insert(i, 23, root[i - 1], root[i]);
    }

    char op[2];
    int l, r, x;
    while (m--)
    {
        scanf("%s", op);
        if (op[0] == 'A')
        {
            scanf("%d", &x);
            n++;
            s[n] = s[n - 1] ^ x;
            root[n] = ++idx;
            insert(n, 23, root[n - 1], root[n]);
        }
        else
        {
            scanf("%d%d%d", &l, &r, &x);
            // 至少要包住第r个点, 所以用r-1, 否则会因为异或把root[r]抵消掉
            // l也同理
            printf("%d\n", query(r - 1, s[n] ^ x, l - 1));
        }
    }
    return 0;
}

2. 可持久化线段树（主席树）

题目链接：

最大异或和

题解思路：

此题可用方法：

  1. 树套树：（$O(mlog^2n)$）支持修改
  2. 划分树：（$O(nlogn)$）不支持修改
  3. 主席树：（$O(nlogn)$）

采用主席树：

核心：把新得点替换掉原来的点,结构一样，信息不一样

  1. 离散化
  2. 在数值上建立线段树，维护每个数值区间个数，求整体第k小的数。

缺点：难以进行区间修改操作

0————-mid————-n-1 mid的左边的个数cnt如果大于k说明第k个数在左边，cnt <= k 说明在右边

此题可以维护每个版本的各个数值区间的个数，因为每个版本结构都是一样的，但是只是信息不同，所以只要用第R个版本减去L-1个版本就可以得到[L， R]这一段这个区间里面0————-mid————-n-1有多少个数。

题目代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
#include <bits/stdc++.h>

using namespace std;
const int N = 100010;
int n, m;
int a[N], root[N], idx;
vector<int> nums;

struct Node{
    int l, r;   //左右孩子，不是区间
    int cnt; //维护数值区间的个数
}tr[N * 4 + N * 17];

int find(int x){
    return lower_bound(nums.begin(), nums.end(), x) - nums.begin(); //返回第一个大于等于x的下标
}

int build(int l, int r){
    int p = ++idx; //一个新得节点
    if(l == r)return p; //叶节点
    int mid = l + r >> 1;
    tr[p].l = build(l, mid), tr[p].r = build(mid + 1, r);
    return p;   
    
}

int insert(int p, int l, int r, int x){
    int q = ++idx; //一个新得节点
    tr[q] = tr[p]; //新节点指向旧节点
    
    if(l == r){     //叶节点
        tr[q].cnt++;    //当前这个值的元素个数+1
        return q;
    }
    int mid = l + r >> 1;
    if(x <= mid) tr[q].l = insert(tr[p].l, l, mid, x);  //元素比中间值小，往左边插入
    else tr[q].r = insert(tr[p].r, mid + 1, r, x);      //元素比中间值大，往右边插入
    tr[q].cnt = tr[tr[q].l].cnt + tr[tr[q].r].cnt;      //父节点的总个数等于左右儿子节点的总个数
    return q;
}

//此题可以维护每个版本的各个数值区间的个数
//因为每个版本结构都是一样的，但是只是信息不同
//所以只要用第R个版本减去L-1个版本就可以得到[L， R]这一段这个区间里面0---------mid---------n-1有多少个数。 
int query(int q, int p, int l, int r, int k){
    if(l == r)return r; //找到
    
    // R版本减去 L-1版本就是【L, R】这个区间中添加的各个数
    int cnt = tr[tr[q].l].cnt - tr[tr[p].l].cnt;  
    
    int mid = l + r >> 1;
    // k <= cnt说明要找的元素在q的左子树里面
    if (k <= cnt) return query(tr[q].l, tr[p].l, l, mid, k);
    else return query(tr[q].r, tr[p].r, mid+1, r, k - cnt);     //减去左半部分总数
}

int main (){
    cin >> n >> m;
    for(int i = 1; i <= n; i++) {
        cin >> a[i];
        nums.push_back(a[i]); //离散化数组
    }
    
    //去重
    sort(nums.begin(), nums.end());
    nums.erase(unique(nums.begin(), nums.end()), nums.end());
    
    root[0] = build(0, nums.size() - 1); //初始化
    
    //相当于n次操作维护各个版本
    for(int i = 1; i <= n; i++){
        //根据前一个版本创建一个新得节点指向前一个版本各个修改的信息
        root[i] = insert(root[i - 1], 0, nums.size() - 1, find(a[i])); 
    }
    
    while(m -- ){
        int l, r, k;
        cin >> l >> r >> k;
        printf("%d\n", nums[query(root[r], root[l - 1], 0, nums.size() - 1, k)]);
    }
    return 0;
    
}

平衡树——Treap

treap、红黑树、splay、sbt、AVL

概念

对于一棵树，我们可以做一些特殊的操作，来让它变换树的形态结构，但是最后的答案却是正确的。平衡树的精髓就是这个，就是改变树的形态结构，但是不改变最后的中序遍历,也就是答案数组。

  1. 首先需要维护一个BST(二叉搜索树)，一个根节点p，左儿子一定小于他，右儿子大于它。

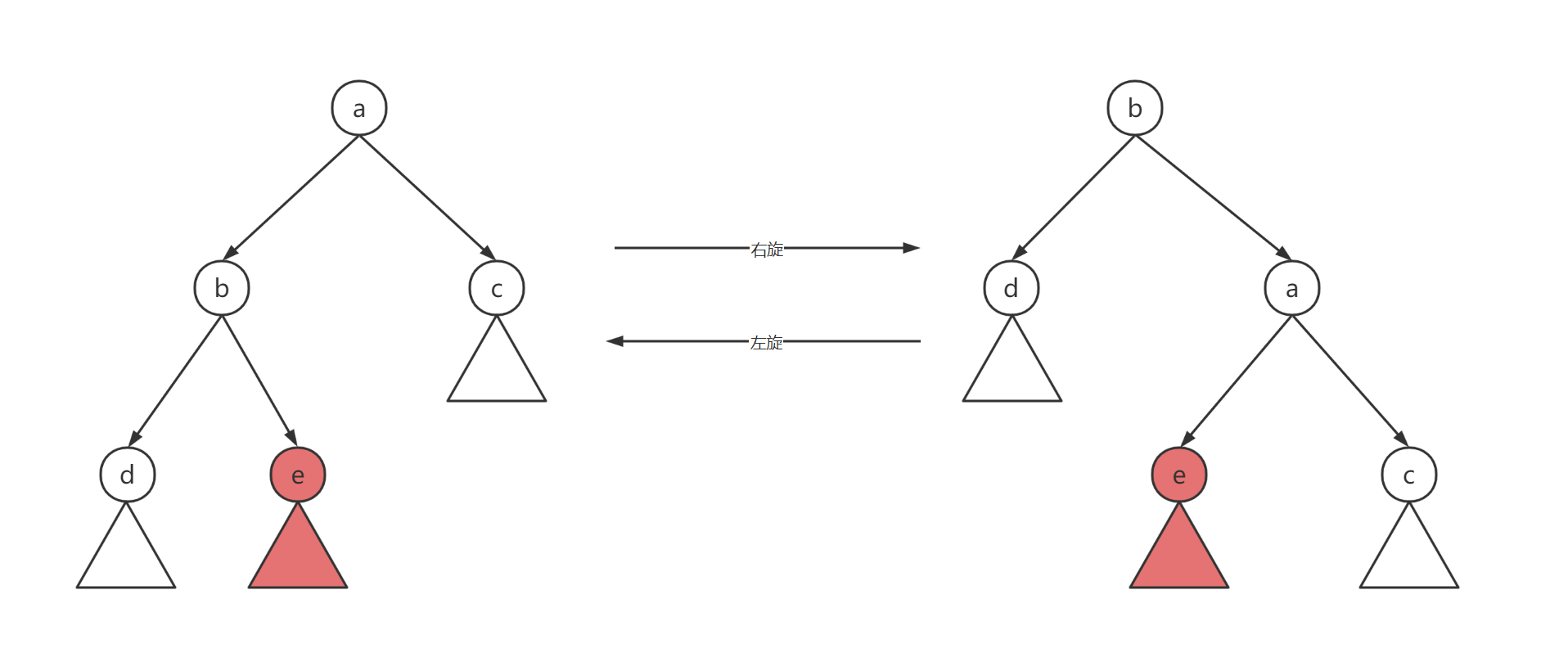
  2. 为了维护这个BST我们需要一个左旋zag和右旋zig，分别表示将根节点和左右儿子交换位置，使交换后还满足BST的性质。

  3. 为了使得这个BST是一个尽可能随机的（添加随机数val维护这个堆）使得这个BST的期望更加好一些（防止出现一条链的情况使得BST的时间复杂度达到O(n)）

操作：

  1. 插入数值 xx。
  2. 删除数值 xx(若有多个相同的数，应只删除一个)。
  3. 查询数值 xx 的排名(若有多个相同的数，应输出最小的排名)。
  4. 查询排名为 xx 的数值。
  5. 求数值 xx 的前驱(前驱定义为小于 xx 的最大的数)。
  6. 求数值 xx 的后继(后继定义为大于 xx 的最小的数)。

1. 普通平衡树

题目链接：

普通平衡树

题解思路：

Treap

  1. 维护键值key——BST，同时维护随机值val——堆
  2. 这样使得这颗树时间复杂度更加趋近于（logn）,防止出现一条链

题目代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
#include<bits/stdc++.h>

using namespace std;

const int N = 100010, INF = 1e8;
int n, root, idx;
struct Node
{
    int l, r;
    int key, val;   //key当前键值，val随机值，使得这个treap更加随机
    int cnt, size;  //cnt当前节点的个数
}tr[N];

void pushup(int u) {
    tr[u].size = tr[tr[u].l].size + tr[tr[u].r].size + tr[u].cnt;//字节点更新父节点信息
}

// 创建一个新得节点
int get_node(int key) { 
    tr[ ++ idx].key = key;  //新得节点的键值
    tr[idx].val = rand();   //随机值，根据这个维护一个堆
    tr[idx].cnt = tr[idx].size = 1; //初始节点的个数等于1，以及当前子树的大小也是1
    return idx;             //返回这个节点所对应的下标
}

// 右旋
void zig(int &p) {
    int q = tr[p].l;
    tr[p].l = tr[q].r, tr[q].r = p, p = q; 
    pushup(tr[p].r), pushup(p);
}

// 左旋
void zag(int &p) {
    int q = tr[p].r;
    tr[p].r = tr[q].l, tr[q].l = p, p = q;
    pushup(tr[p].l), pushup(p);
}

// 初始化
void build() {
    get_node(-INF), get_node(INF);  //创建两个哨兵
    root = 1, tr[1].r = 2;          
    pushup(root);                   //更新
    if (tr[1].val < tr[2].val) zag(root);   //父节点的val < 右子节点的val左旋
}

void insert(int &p, int key) {
    if (!p) p = get_node(key);                      //如果之前没有的话就创建一个新得节点
    else if (tr[p].key == key) tr[p].cnt ++ ;       //如果之前存在就直接再cnt++
    else if (tr[p].key > key)                       //key小于当前节点的值往左边递归插入
    {
        insert(tr[p].l, key);
        if (tr[tr[p].l].val > tr[p].val) zig(p);    //需要维护val    
    } else {                                        //key大于当前节点的值往右边递归插入
        insert(tr[p].r, key);
        if (tr[tr[p].r].val > tr[p].val) zag(p);
    }
    pushup(p);  //更新
}

void remove(int &p, int key) {
    if (!p) return;         //不存在这个点，直接返回
    if (tr[p].key == key) {     
        if (tr[p].cnt > 1) tr[p].cnt -- ;   //这个点的数量大于1，数量--
        else if (tr[p].l || tr[p].r) {      //这个点左右子树都不空
            if (!tr[p].r || tr[tr[p].l].val > tr[tr[p].r].val) {    //右旋
                zig(p);
                remove(tr[p].r, key);
            }
            else {                          //左旋
                zag(p);
                remove(tr[p].l, key);
            }
        }
        else p = 0; //叶子节点，左右子树都空
    }
    else if (tr[p].key > key) remove(tr[p].l, key);
    else remove(tr[p].r, key);

    pushup(p);  //更新
}

// 通过数值找排名
int get_rank_by_key(int p, int key) {
    if (!p) return 0;   
    if (tr[p].key == key) return tr[tr[p].l].size + 1;
    if (tr[p].key > key) return get_rank_by_key(tr[p].l, key);
    return tr[tr[p].l].size + tr[p].cnt + get_rank_by_key(tr[p].r, key);
}

// 通过排名找数值
int get_key_by_rank(int p, int rank) {
    if (!p) return INF;     
    if (tr[tr[p].l].size >= rank) return get_key_by_rank(tr[p].l, rank);    
    if (tr[tr[p].l].size + tr[p].cnt >= rank) return tr[p].key;
    return get_key_by_rank(tr[p].r, rank - tr[tr[p].l].size - tr[p].cnt);
}

// 找到严格小于key的最大数
int get_prev(int p, int key) {
    if (!p) return -INF;
    if (tr[p].key >= key) return get_prev(tr[p].l, key);
    return max(tr[p].key, get_prev(tr[p].r, key));
}

// 找到严格大于key的最小数
int get_next(int p, int key) {
    if (!p) return INF;
    if (tr[p].key <= key) return get_next(tr[p].r, key);
    return min(tr[p].key, get_next(tr[p].l, key));
}


int main(){
    build();
    cin >> n;
    while (n -- ) {
        int op, x;
        cin >> op >> x;
        if (op == 1) insert(root, x);
        else if (op == 2) remove(root, x);
        else if (op == 3) cout << get_rank_by_key(root, x) - 1 << endl;
        else if (op == 4) cout << get_key_by_rank(root, x + 1) << endl;
        else if (op == 5) cout << get_prev(root, x) << endl;
        else cout << get_next(root, x) << endl;
    }

    return 0;
}

2. 营业额统计

题目链接：

营业额统计

题解思路：

可以用set的lower_bound(), upper_bound()

也可用平衡树

题目代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
#include <bits/stdc++.h>
typedef long long ll;
using namespace std;

const int N = 33000, INF = 1e7;

struct Node{
    int l, r;
    int key, val;
}tr[N];

int root, idx, n;

//创建新得节点
int get_node(int key){
    tr[++idx].key = key;
    tr[idx].val = rand(); //使得平衡树更加随机，期望更高
    return idx;
}

//初始化
void build(){
    get_node(-INF), get_node(INF);
    root = 1, tr[1].r = 2;
}

//右旋
void zig(int &p){
    int q = tr[p].l;
    tr[p].l = tr[q].r, tr[q].r = p, p = q;
}

//左旋
void zag(int &p){
    int q = tr[p].r;
    tr[p].r = tr[q].l, tr[q].l = p, p = q;
}

//插入操作
void insert(int &p, int key){
    if(!p) p = get_node(key); //没有这个节点就直接创建这个节点
    else if(tr[p].key == key) return;   //之前有这个节点
    else if(tr[p].key > key){           //插入到当前节点左边
        insert(tr[p].l, key); 
        if(tr[tr[p].l].val > tr[p].val) //检查子节点的val是否大于父节点
            zig(p);                     //右旋
    }
    else{
        insert(tr[p].r, key);
        if(tr[tr[p].r].val > tr[p].val) //检查子节点的val是否大于父节点
            zag(p);                     //左旋
    }
}

//找到小于等于key的最大数
int get_prev(int p, int key){
    if(!p) return -INF;
    if(tr[p].key > key) return get_prev(tr[p].l, key); //往左边查找
    else return max(tr[p].key, get_prev(tr[p].r, key)); //右边
}

//找到大于等于key的最小的数
int get_next(int p, int key) {
    if (!p) return INF;
    if (tr[p].key < key) return get_next(tr[p].r, key);
    return min(tr[p].key, get_next(tr[p].l, key));
}


int main ()
{
    build();
    cin >> n;
    ll res = 0;
    for(int i = 1; i <= n; i++){
        int x;
        cin >> x;
        if(i == 1)res += x;
        else{
            res += min(x - get_prev(root, x), get_next(root, x) - x); //x与x的前一个值的差值，x与后一个值的差值
        }
        
        insert(root, x);
    }
    cout << res << endl;
    return 0;
}

AC自动机

ac自动机 = trie + kmp

next[i]: 在p中以p[i]结尾的后缀，能够匹配从1开始的（非平凡）前缀的最大长度

ac自动机就是对trie求next

用BFS的思想，一层一层遍历，对应于一维求next数组

1. 搜索关键词

题目链接：

搜索关键词

题解思路：

用BFS的思想，一层一层遍历，对应于一维求next数组

题目代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include <bits/stdc++.h>

using namespace std;
const int N = 10010, S = 55, M = 1000010;

int n;
int tr[N * S][26], cnt[N * S], idx;
char str[M];
int q[N * S], ne[N * S], tt;

//trie树插入操作
void insert() {
    int p = 0;
    for (int i = 0; str[i]; i ++ ) {
        int t = str[i] - 'a';
        if (!tr[p][t]) tr[p][t] = ++ idx; //创建一个节点
        p = tr[p][t];
    }
    cnt[p] ++ ; //此节点个数++
}

//等价于处理next数组
void build() {
    int hh = 0, tt = -1;
    for (int i = 0; i < 26; i ++ )
        if (tr[0][i])   //如果第一个字母没有就不用入队
            q[ ++ tt] = tr[0][i];

    while (hh <= tt) {
        int t = q[hh ++ ];
        for (int i = 0; i < 26; i ++ ) {    //遍历当前节点的所有子节点
            int c = tr[t][i];   //对应当前节点
            if(!c)continue;
            int j = ne[t];      //对应前面的状态，也就是前面的层
            while(j && !tr[j][i]) j =  ne[j];   //如果这个节点是空的话就查找ne数组
            if(tr[j][i]) j = tr[j][i];
            ne[c] = j;
            q[++tt] = c;
        }
    }
}

int main () {
    int T;
    cin >> T;
    while(T--){
        memset(tr, 0, sizeof tr);
        memset(cnt, 0, sizeof cnt);
        memset(ne, 0, sizeof ne);
        idx = 0;
        cin >> n;
        for(int i = 1; i <= n; i++){
            scanf("%s", str);
            insert();
        }
        build();
        scanf("%s", str);
        int res = 0;
        for(int i = 0, j = 0; str[i]; i++){
            int t = str[i] - 'a';
            while(j && !tr[j][t]) j = ne[j];    
            if(tr[j][t]) j = tr[j][t];
            int p = j;
            while(p){
                res += cnt[p];
                cnt[p] = 0;
                p = ne[p];
            }
        }
        cout << res << endl;
    }

    return 0;
}

可以优化成一个trie图

将空节点的指针指向它父节点的next指向的位置，这样就相当于每个空姐点都会直接指向它对应得next节点上去

有点路径压缩的感觉

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
#include <bits/stdc++.h>

using namespace std;
const int N = 10010, S = 55, M = 1000010;

int n;
int tr[N * S][26], cnt[N * S], idx;
char str[M];
int q[N * S], ne[N * S], tt;

//trie树插入操作
void insert() {
    int p = 0;
    for (int i = 0; str[i]; i ++ ) {
        int t = str[i] - 'a';
        if (!tr[p][t]) tr[p][t] = ++ idx; //创建一个节点
        p = tr[p][t];
    }
    cnt[p] ++ ; //此节点个数++
}

//等价于处理next数组
void build() {
    int hh = 0, tt = -1;
    for (int i = 0; i < 26; i ++ )
        if (tr[0][i])   //如果第一个字母没有就不用入队
            q[ ++ tt] = tr[0][i];

    while (hh <= tt) {
        int t = q[hh ++ ];
        for (int i = 0; i < 26; i ++ ) {    //遍历当前节点的所有子节点
            int p = tr[t][i];               //对应当前节点
            if(!p) tr[t][i] = tr[ne[t]][i]; //直接跳到对应得位置，有点路径压缩的感觉
            else{
                ne[p] = tr[ne[t]][i];       
                q[++ tt] = p;
            }
        }
    }
}

int main () {
    int T;
    cin >> T;
    while(T--){
        memset(tr, 0, sizeof tr);
        memset(cnt, 0, sizeof cnt);
        memset(ne, 0, sizeof ne);
        idx = 0;
        cin >> n;
        for(int i = 1; i <= n; i++){
            scanf("%s", str);
            insert();
        }
        build();
        scanf("%s", str);
        int res = 0;
        for(int i = 0, j = 0; str[i]; i++){
            int t = str[i] - 'a';
            j = tr[j][t]; //下一个节点
            int p = j;
            while(p){       //下一个节点，不为空
                res += cnt[p];
                cnt[p] = 0;
                p = ne[p];
            }
        }
        cout << res << endl;
    }

    return 0;
}

2. 单词

题目链接：

单词

题解思路：

去求所有满足要求的前缀个数：

所有满足要求的前缀其后缀一定等于原串单词。

需要反向来求：

trie是通过next指针，根据地推的思想一直往前推，next可以求出前一个满足要求的前缀（可以和后缀匹配），可以一直跟着next指针一直往前走。

对于i来说可以用next指针将f[i] 累加到f[next[i]]上去，f的累加相当于是有向无环图，所有的和都会累加到终止节点上去，可以用拓扑排序的方法来求最终节点。

题目代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include <bits/stdc++.h>

using namespace std;
const int N = 1000010;
int n;
int tr[N][26], f[N], q[N], ne[N], idx;
char str[N];
int id[210];   //单词编号 


//插入操作
void insert(int x){
    int p = 0;
    for(int i = 0; str[i]; i ++){
        int t = str[i] - 'a';
        if(!tr[p][t]) tr[p][t] = ++idx;    //创建新的节点
        p = tr[p][t];
        f[p] ++;    //每一个结束位置都代表一个字符串
    }
    id[x] = p;  //记录每个单词结尾所在地方
}

void build(){
    int hh = 0, tt = -1;
    for(int i = 0; i < 26; i++){
        if(tr[0][i])q[++tt] = tr[0][i];
    }
    while(hh <= tt){
        int t = q[hh++];
        for(int i = 0; i < 26;i ++){
            int &p = tr[t][i];
            if(!p) p = tr[ne[t]][i];
            else{
                ne[p] = tr[ne[t]][i];
                q[++tt] = p;
            }
        }
    }
}


int main ()
{
    cin >> n;
    for(int i = 0; i < n; i++){
        scanf("%s", str);
        insert(i);
    }
    
    build();
    
    //上面是从根节点一层一层求得，所以拓扑排序是倒序
    for (int i = idx - 1; i >= 0; i -- ) f[ne[q[i]]] += f[q[i]];    

    for (int i = 0; i < n; i ++ ) printf("%d\n", f[id[i]]);
    
    return 0;
    
}